Combinatoire énumérative
Combinatoire énumérative
I Rappels de théorie des ensembles
I Rappels de théorie des ensembles
Combinatoire énumérative
→ I Rappels de théorie des ensembles
I-2 Entiers naturels, récurrence
I-1 Applications
Combinatoire énumérative
→
I Rappels de théorie des ensembles
→ I-1 Applications
Une application (ou fonction) d'un ensemble dans un ensemble , notée , est la donnée, pour chaque élément de d'un élément de . L'ensemble est appelé ensemble de départ et l'ensemble est l'ensemble d'arrivée. L'élément est l'image de par . On écrit aussi . Un exemple trivial d'application est l'application identique de , notée telle que . Si et sont deux applications, l'application composée de et est
Si est une partie de , on note et on nomme image de par la partie
de formée des éléments de dont l'image est dans . Par extension, si est un élément de , on note l'image réciproque du singleton . C'est donc l'ensemble des éléments de dont l'image par est . Cet ensemble peut être vide. On dit que l'application est surjective, ou que c'est une surjection si elle n'est vide pour aucune valeur de et qu'elle est injective, ou que c'est une injection s'il n'a plus d'un élément pour aucune valeur de :
Définition
Une application
est
-
injective si et seulement si
-
surjective si et seulement si
-
bijective si et seulement si elle est à la fois injective et surjective.
En résumé, est bijective si et seulement si pour tout de , l'ensemble a un élément et un seul, que l'on note encore . On voit facilement que est alors une bijection de dans et que l'on a et . On dit que est la bijection réciproque de .
Il existe une autre notation courante pour les applications. La notation désigne une famille d'éléments de indexée par l'ensemble . Il s'agit simplement d'une application de dans , où est l'image de par l'application.
I-2 Entiers naturels, récurrence
Combinatoire énumérative
→
I Rappels de théorie des ensembles
→ I-2 Entiers naturels, récurrence
Nous admettrons l'existence d'un ensemble
Ce principe est en général utilisé de la façon suivante. Soit un prédicat sur , c'est-à-dire une propriété qui, pour chaque entier naturel, peut être vraie ou fausse. Si on a établi que est vrai et si pour quelconque, en supposant on a prouvé , alors est vrai pour tout . On applique pour cela l'énoncé ci-dessus à la partie de formée des tels que est vrai.
On peut déduire de ce principe la
Proposition [construction par récurrence]
Si
est une application et
un élément de
, il existe une application
et une seule telle que
et
.
Une famille indexée par les entiers naturels s'appelle une suite. L'application ci-dessus est souvent notée sous forme de suite. On pose et on dit que la suite est définie par récurrence par les relations et .
L'ensemble est alors muni de trois lois de composition c'est-à-dire d'applications de dans appelées addition, multiplication et exponentiation et notées respectivement , ou et . La construction se fait en utilisant le principe de récurrence et les relations
- .
En d'autres termes, l'addition est définie par récurrence à partir de l'application , la multiplication par récurrence à partir de l'addition et l'exponentiation par récurrence à partir de la multiplication. Retenons en particulier que .
Si et sont deux entiers naturels, on dit que est inférieur ou égal à et on note s'il existe tel que . On montre que c'est une relation d'ordre c'est-à-dire que l'on a
La relation d'ordre sur est un bon ordre, c'est-à-dire que l'on a:
Proposition
Toute partie non vide de
a un plus petit élément.
Démonstration
Soit
une partie de
dont on suppose qu'elle n'a pas de plus petit élément. On pose
l'ensemble des minorants stricts de . Comme est le plus petit élément de , il ne peut appartenir à et on a . D'autre part, si on a pour tout dans . Cela implique mais impliquerait que est le plus petit élément de . On a donc et . En application du principe de récurrence, on a , donc , ce qui termine la preuve.
Si et sont deux entiers naturels, on notera
En particulier, lorsque , est l'ensemble vide .
I-3 Le cardinal d'un ensemble
Combinatoire énumérative
→
I Rappels de théorie des ensembles
→ I-3 Le cardinal d'un ensemble
L'existence d'une injection de dans peut être interprétée comme `` est plus petit que ''. Le résultat suivant permet de donner un sens précis à cette intuition.
Théorème [de Cantor-Bernstein]
Soient
et
deux ensembles. S'il existe une injection de
dans
et une injection de
dans
, alors il existe une bijection de
dans
.
Démonstration
On définit par récurrence deux suites de parties de
par
,
,
et
. On voit par récurrence que ces parties sont ``emboîtées'':
On pose
et on définit une application par s'il existe un entier tel que et sinon. Il reste à vérifier que est une bijection.
De même que la couleur bleue est simplement ce qu'ont en commun tous les objets bleus, le cardinal d'un ensemble , noté , est ce qu'ont en commun des ensembles qui sont en bijection. En d'autres termes, on dit que et ont même cardinal si et seulement si il existe une bijection de dans . On peut comparer les cardinaux: on dit que le cardinal de est inférieur ou égal à celui de , et on note si et seulement si il existe une injection de dans . Grâce au théorème de Cantor-Bernstein, on a la
Proposition
Si
et
sont des ensembles,
L'énoncé précédent pourrait paraître évident, sauf que les cardinaux ne sont pas en général des nombres, au sens où on l'entend généralement. Par exemple, un cardinal peut être infini.
Plutôt que d'utiliser les injections pour comparer les ensembles, on aurait pu utiliser les surjections. En fait on a la
Proposition
Soient
et
deux ensembles. Les deux propriétés suivantes sont équivalentes
- Il existe une injection de dans .
- est vide ou il existe une surjection de sur
Démonstration
Si
n'est pas vide, choisissons un élément
de
. Si
existe, on définit
par
Si existe, on définit en choisissant pour n'importe quel élément de .
I-4 Ensembles finis
Combinatoire énumérative
→
I Rappels de théorie des ensembles
→ I-4 Ensembles finis
Un ensemble est dit fini s'il existe une bijection de sur un intervalle entier . S'il n'est pas fini, il est dit infini. On va voir que est alors unique.
Théorème
Soient
et
deux entiers naturels.
- [i)] Il existe une injection de dans si et seulement si .
- [ii)] Il existe une surjection de sur si et seulement si ou .
- [iii)] Il existe une bijection de sur si et seulement si .
En particulier, si est un ensemble fini, il existe un entier naturel et un seul tel que est en bijection avec . Au lieu de noter , on notera et on dira que le cardinal de est .
Démonstration
Démontrons la propriété i) par récurrence sur
et indépendamment de
, c'est-à-dire appelons
la propriété de
qui dit que cette assertion est vraie pour tout
.
Comme
, il y a toujours une injection de
dans
et
est toujours vrai.
Donc
est vrai. Supposons
et considérons une injection
de
dans
. Supposons d'abord
. On a forcément
. Puisque
est injectif, l'image de
par
est inclus dans
.
La restriction de
à
, c'est-à-dire l'application de
dans
qui coïncide avec
est une injection, et l'hypothèse de récurrence implique
et
.
Dans le cas où , il existe une bijection de
dans lui-même qui échange
et
et laisse fixes tous les autres éléments. La composée
est encore une injection de
dans
, et vérifie
. On a donc encore
et P(n+1) est vrai, ce qui achève de démontrer le i). Mais le ii) est exactement équivalent à i) en échangeant
et
. Enfin i) et ii) donnent iii).
de
dans lui-même qui échange
et
et laisse fixes tous les autres éléments. La composée
est encore une injection de
dans
, et vérifie
. On a donc encore
et P(n+1) est vrai, ce qui achève de démontrer le i). Mais le ii) est exactement équivalent à i) en échangeant
et
. Enfin i) et ii) donnent iii).
Dans le cas où , il existe une bijection
 de
dans lui-même qui échange
et
et laisse fixes tous les autres éléments. La composée
est encore une injection de
dans
, et vérifie
. On a donc encore
et P(n+1) est vrai, ce qui achève de démontrer le i). Mais le ii) est exactement équivalent à i) en échangeant
et
. Enfin i) et ii) donnent iii).
de
dans lui-même qui échange
et
et laisse fixes tous les autres éléments. La composée
est encore une injection de
dans
, et vérifie
. On a donc encore
et P(n+1) est vrai, ce qui achève de démontrer le i). Mais le ii) est exactement équivalent à i) en échangeant
et
. Enfin i) et ii) donnent iii).
Le théorème précédent justifie la notation
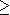 employée en deux sens différents, l'un pour les entiers, l'autres pour les cardinaux. Ces deux acceptions sont compatibles. On peut reformuler le théorème précédent de plusieurs manières.
employée en deux sens différents, l'un pour les entiers, l'autres pour les cardinaux. Ces deux acceptions sont compatibles. On peut reformuler le théorème précédent de plusieurs manières.Théorème [principe des tiroirs]
Si
est une application et
et
sont des ensembles (finis) tels que
, alors
n'est pas injective.
Si on a plus d'objets que de tiroirs, quel que soit le rangement on est obligé de ranger deux objets dans le même tiroir.
Théorème [principe d'inclusion]
Si
est un ensemble fini et
une partie de
, alors
est fini et
. Si, de plus, on a
, alors
.
I-5 Cardinaux infinis
Combinatoire énumérative
→
I Rappels de théorie des ensembles
→ I-5 Cardinaux infinis
Proposition
Pour tout ensemble infini
, il existe une injection de
dans
.
On dit que est dénombrable s'il a même cardinal que . C'est le plus petit infini possible:
Certains ensembles classiques sont dénombrables, comme , , l'ensemble des nombres rationnels, ou l'ensemble des parties finies de .
Mais il existe des cardinaux infinis plus grands. Par exemple, l'ensemble des nombres réels n'est pas dénombrable.
Il est facile de montrer qu'il y a une infinité de cardinaux infinis distincts à l'aide du théorème suivant.
Théorème
Soit
un ensemble. Il n'y a pas d'application surjective (donc pas de bijection) de
dans l'ensemble
des parties de
.
Démonstration
Soit
 une application de
dans
. Posons
une application de
dans
. Posons
 , et
, et
 n'est pas surjective.
n'est pas surjective.
 une application de
dans
. Posons
une application de
dans
. Posons
Supposons qu'il existe tel que . On peut donc écrire
ce qui est une contradiction. On a donc prouvé que n'appartient pas à l'image de
 , et
, et
 n'est pas surjective.
n'est pas surjective.
I-6 Relations binaires
Combinatoire énumérative
→
I Rappels de théorie des ensembles
→ I-6 Relations binaires
Une relation binaire sur un ensemble est un prédicat sur , c'est-à-dire une propriété que possède ou ne possède pas chaque couple d'éléments de . S'il possède la propriété, on dit que est en relation avec et on note . La relation est réflexive si et seulement si
La relation inverse ou opposée à est la relation telle que
La relation est symétrique si et seulement si
c'est-à-dire . Elle est antisymétrique si et seulement si
La clôture symétrique de la relation est la relation définie par
Elle est évidemment symétrique. La relation est transitive si et seulement si
La clôture réflexive-transitive de la relation est la relation définie par
c'est-à-dire que l'on peut passer de à en un nombre fini d'étapes, chaque élément étant en relation avec le suivant le long du chemin. La relation est bien sûr réflexive et transitive.
La relation est une relation d'ordre si et seulement si elle est réflexive, antisymétrique et transitive. C'est une relation d'équivalence si elle est réflexive, symétrique et transitive.
Si est une application, la relation définie par
est une relation d'équivalence. En fait, toute relation d'équivalence est obtenue de cette manière. Si est une relation d'équivalence sur , on associe à chaque sa classe d'équivalence qui est une partie non vide de . L'ensemble des classes d'équivalence, noté est une partition de , c'est-à-dire une famille de parties non vides de , disjointes deux à deux et dont la réunion est . L'application redonne par le procédé décrit au début de ce paragraphe.
II Outils de base
Combinatoire énumérative
→ II Outils de base
On a vu qu'une des propriétés les plus fondamentales d'un ensemble fini est son cardinal, un entier naturel. L'objet général de la combinatoire énumérative est de ``calculer'' ce cardinal pour des ensembles particuliers. La plupart du temps, l'ensemble considéré dépend d'un ou plusieurs paramètres, et il s'agit d'exprimer ce cardinal comme fonction de ces paramètres. Nous serons ainsi amenés à définir certaines fonctions de ou dans , en commençant avec les opérations de base définies plus haut.
Un autre but naturel de cet étude est de montrer que certains ensembles finis ont même cardinal. Une méthode pour prouver que est de calculer et séparément, puis de comparer les résultats. C'est ce que l'on appelle une preuve par le calcul, ou calculatoire. Il est aussi souvent possible de construire explicitement une bijection entre et . On a dans ce cas une preuve combinatoire. De manière générale les mathématiciens préfèrent les preuves combinatoires pour deux raisons en fait liées: elles donnent en général une idée de ``la raison pour laquelle'' alors que les preuves calculatoires suggèrent rarement des idées nouvelles, et elles sont souvent plus satisfaisantes d'un point de vue esthétique.
II-1 Les opérations de base sur les cardinaux
II-2 Fonctions caractéristiques
II-3 Sommes et produits dans un anneau commutatif
II-5 Arrangements, permutations et combinaisons
II-6 Les coefficients multinomiaux
II-1 Les opérations de base sur les cardinaux
Combinatoire énumérative
→
II Outils de base
→ II-1 Les opérations de base sur les cardinaux
Théorème [Union disjointe]
Si
et
sont deux ensembles finis disjoints, l'ensemble
est fini et l'on a
Démonstration
Par récurrence sur
. Si
,
est vide et
a bien pour cardinal
.
Si
, il existe une bijection
de
dans
. Posons
. La restriction de
à
est une bijection de
sur
. On en déduit que
, et, par hypothèse de récurrence,
. Il y a donc une bijection
de
dans
. On pose
et on vérifie que
devient une bijection de
sur
, ce qui achève la récurrence.
Théorème [Produit]
Si
et
sont des ensembles finis, leur produit cartésien
est fini, et l'on a
Démonstration
Par récurrence sur
. Si
,
est vide et
aussi. On a donc bien
Si
, on reprend les notations de la démonstration précédente. Comme
est réunion disjointe de
et de
. Ce dernier ensemble est en bijection avec
par l'application
qui à
fait correspondre le couple
. Il est donc de cardinal
et en appliquant le théorème précédent on a
, ce qui achève la démonstration.
Corollaire [Principe des bergers]
Soit
un ensemble fini,
une application et
un entier naturel non nul. On suppose que
Alors est fini et .
Démonstration
Pour chaque
dans
, numérotons de 1 à
les éléments de
. L'application qui à
fait correspondre le
-ème élément de
est alors une bijection de
sur
.
Ce principe est souvent appliqué pour calculer le cardinal de . À chaque élément d'un ensemble de pattes, on fait correspondre le mouton du troupeau auquel elle est attachée. Comme chaque mouton a (en principe) 4 pattes, on peut en déduire qu'il y a 4 fois plus de pattes que de moutons, ou 4 fois moins de moutons que de pattes. Cela peut être pratique si l'on voit les pattes mais pas les moutons.
Théorème [Ensemble puissance]
Si
et
sont des ensembles finis, alors l'ensemble
des applications de
dans
est fini et l'on a
Démonstration
Par récurrence sur
. Si
,
est vide et il existe exactement une application de
dans
: à chaque élément de
est associé un élément de
et ceci ne peut être fait que d'une seule façon. On a donc bien
.
Si
, on reprend les notations de la démonstration précédente.
Ë chaque application
de
dans
, faisons correspondre le couple
, où
est la restriction de
à
et
. L'application
 est une bijection de
sur
. En appliquant successivement le théorème précédent, l'hypothèse de récurrence et la définition de l'exponentiation, on trouve bien
est une bijection de
sur
. En appliquant successivement le théorème précédent, l'hypothèse de récurrence et la définition de l'exponentiation, on trouve bien
 est une bijection de
sur
. En appliquant successivement le théorème précédent, l'hypothèse de récurrence et la définition de l'exponentiation, on trouve bien
est une bijection de
sur
. En appliquant successivement le théorème précédent, l'hypothèse de récurrence et la définition de l'exponentiation, on trouve bien
ce qui achève la démonstration.
II-2 Fonctions caractéristiques
Combinatoire énumérative
→
II Outils de base
→ II-2 Fonctions caractéristiques
Soit un ensemble et une partie de . On appelle fonction caractéristique de et on note la fonction de dans l'ensemble définie par
Proposition
Si
, alors
.
Les opérations d'intersection, de passage au complémentaire et de réunion se traduisent naturellement en termes de fonctions caractéristiques:
Proposition
- ,
- ,
- .
Nous verrons plus loin une généralisation de cette dernière formule. Le cardinal d'une partie finie peut s'écrire en termes de fonctions caractéristiques:
Proposition
Pour toute partie
d'un ensemble (fini)
, on a
II-3 Sommes et produits dans un anneau commutatif
Combinatoire énumérative
→
II Outils de base
→ II-3 Sommes et produits dans un anneau commutatif
- ,
- ,
- ,
- ,
- ,
- ,
- ,
- .
Dans un anneau commutatif, on peut définir la somme ainsi que le produit d'une famille finie d'éléments: une somme vide vaut 0 et un produit vide vaut 1, puis, par récurrence, on définit
et
Comme les opérations sont commutatives, on ne se préoccupe pas de l'ordre des opérandes et on peut écrire simplement ou dès lors que l'ensemble d'indices est fini. On peut dans ce cadre ``développer un produit'':
Proposition [Formule du produit]
Soient
et
deux familles finies d'éléments d'un anneau commutatif
. On a
la somme étant indexée par les parties de de .
L'idée de cette proposition est que si l'on utilise autant de fois que possible la relation de distributivité pour développer le produit, on se retrouve avec une somme de termes. Chacun de ces termes est produit de facteurs, un facteur provenant de chacune des sommes et valant donc soit soit . En notant l'ensemble des indices pour lesquels on a choisi plutôt que , on voit que chaque terme correspond a une partie de et une seule, et que le terme correspondant à est bien .
La preuve suivante est là seulement pour respecter le règlement...
Démonstration
Par récurrence sur
. Pour
, il suffit de voir que
est l'unique partie de
 . La somme de droite a donc exactement un terme, qui est un produit vide comme la partie gauche de l'équation. On est donc ramené à
qui est vrai.
. La somme de droite a donc exactement un terme, qui est un produit vide comme la partie gauche de l'équation. On est donc ramené à
qui est vrai.
En supposant la relation vraie pour , on a
ce qui constitue la relation pour
et achève la preuve par récurrence. Le passage de la quatrième ligne à la cinquième se fait en posant
dans la première somme et
dans la seconde.
 . La somme de droite a donc exactement un terme, qui est un produit vide comme la partie gauche de l'équation. On est donc ramené à
qui est vrai.
. La somme de droite a donc exactement un terme, qui est un produit vide comme la partie gauche de l'équation. On est donc ramené à
qui est vrai.
En supposant la relation vraie pour , on a
II-4 La formule du binôme
Combinatoire énumérative
→
II Outils de base
→ II-4 La formule du binôme
c'est-à-dire que le terme correspondant à ne dépend que du cardinal qui est un entier compris entre et . Il est alors naturel de regrouper entre eux les termes correspondant à la même valeur de . Cela amène à définir les coefficients binômiaux. Pour tout couple d'entiers naturels et , on note et on prononce `` parmi '' le nombre de parties à éléments dans un ensemble à éléments. On a donc la
Proposition [formule du binôme]
Il est utile de pouvoir calculer ces coefficients. Pour , il s'agit de compter les parties de l'ensemble vide. Il y en a une seule, et son cardinal est 0. On a donc
De façon générale, il est clair que est nul sauf si . On peut donc convenir que pour . On a alors la
Proposition
Démonstration
Posons
L'application
est une bijection de
sur
. Les ensembles
et
coïncident, et
est réunion disjointe de
et
. On a donc
et les coefficients du binôme peuvent se calculer par récurrence.
En pratique, la méthode ci-dessus est celle qui est employée pour calculer les coefficients du binôme et construire ce qu'on appelle le triangle de Pascal, c'est-à-dire une table de ces coefficients, généralement arrangée comme ci-dessous.
chaque terme étant somme de celui qui est immédiatement au dessus et de celui qui est à gauche de celui-là. Les cases vides contiennent la valeur 0.
II-5 Arrangements, permutations et combinaisons
Combinatoire énumérative
→
II Outils de base
→ II-5 Arrangements, permutations et combinaisons
La factorielle d'un entier est définie (par récurrence) par la formule
On peut exprimer à l'aide de factorielles le nombre de -arrangements ou injections de dans :
Proposition
Démonstration
La deuxième égalité étant évidente, prouvons la première par récurrence sur
. Il y a une seule injection de l'ensemble vide dans
et le produit vide
vaut 1. L'égalité est donc vraie pour
. Supposons la relation vraie pour
. Ë chaque injection
de
dans
on fait correspondre
, sa restriction à
qui est une injection de
dans
. L'image réciproque
est formée des
qui ont même valeur que
sur
. Il y en a autant que de valeurs possibles pour
, c'est-à-dire n'importe quel élément de
différent des
valeurs prises par
. Il y a donc
éléments dans
. On déduit donc du principe des bergers que
d'où le résultat.
Le cas particulier mérite d'être considéré à part. On appelle permutation d'un ensemble une bijection de dans lui-même. Pour tout entier naturel , on note l'ensemble des permutations de :
Corollaire
On peut maintenant compter le nombre de -combinaisons, c'est-à-dire de parties de cardinal , de :
Proposition
Démonstration
Nous allons donner deux preuves distinctes de cette importante relation. La première est une application du principe des bergers. Ë chaque injection
de
dans
, faisons correspondre son image
. C'est une partie de
de cardinal
. Si
est une partie de
de cardinal
, il existe une bijection
de
sur
. L'ensemble
est formé des
, où
 parcourt
.
On a donc
pour
. Il reste les cas
et
pour lesquels les deux membres valent 1.
parcourt
.
On a donc
pour
. Il reste les cas
et
pour lesquels les deux membres valent 1.
 parcourt
.
On a donc
parcourt
.
On a donc
et le principe des bergers donne
d'où la proposition. L'autre démonstration est par récurrence sur . Le cas est immédiat. Un calcul simple donne
II-6 Les coefficients multinomiaux
Combinatoire énumérative
→
II Outils de base
→ II-6 Les coefficients multinomiaux
comme le nombre de -uplets de parties disjointes de telles que .
Proposition
Soit
un
-uplet d'éléments d'un anneau commutatif et
un entier naturel. On a
On a pour ces coefficients une formule analogue à celle des coefficients binomiaux
et dans le cas , on retrouve les coefficients du binôme
Proposition
Si
, on a
II-7 La formule du crible
Combinatoire énumérative
→
II Outils de base
→ II-7 La formule du crible
et de même
Dans le cas général, on a la formule du crible.
Théorème [Formule du crible]
Si
est une famille de
parties d'un ensemble fini
, leur réunion a pour cardinal
Ce théorème est aussi appelé principe d'inclusion-exclusion.
Démonstration
Dans l'anneau
des fonctions de
dans
, posons
et
, de façon que
, et appliquons la formule du produit:
En effet, le terme correspondant à
vaut 1. On élimine ce terme et on change de signe pour obtenir
Il reste à calculer la somme des valeurs de ces deux fonctions
II-8 Surjections
Combinatoire énumérative
→
II Outils de base
→ II-8 Surjections
Grâce à la formule du crible, on peut compter le nombre de surjections de dans . Notons l'ensemble des applications de dans . On a vu que . Pour tout , notons
l'ensemble des applications de dans . La réunion des est l'ensemble des applications de dans qui ne sont pas surjectives. Il y en a donc . Pour tout , on a
et ne dépend que du cardinal . La formule du crible donne donc
On a donc montré la
Proposition
Explicitons le cas . On a
et on vérifie bien que pour et puisqu'une surjection de dans lui-même est automatiquement une bijection.